So just what is the estimation of uncertainty of measurement? I am so happy you asked. While the term might take you back to the old acronym ‘WAG’ (Wild Ass Guess) the International Organization for Standardization ISO 17025, “General Requirements for the Competence of Testing and Calibration Laboratories” has emphasized the mandatory requirement for all testing & calibration laboratories to apply procedures for close ‘estimation of uncertainty measurement’. It is compulsory for testing & calibration laboratories when submitting final test /calibration results; labs should also attach an enclosed statement about the best closest estimated uncertainty of measurement, keeping it most relevant to the validity of results. All the general requirements for the estimation of uncertainty of measurement and reporting has been mentioned in ISO 17025.
Definition of Uncertainty in ‘Estimation of Uncertainty of Measurement’ as Defined by ISO
Uncertainty – is defined by ISO (International Vocabulary of Basic and General Terms in Metrology) as the parameter, associated with the result of a measurement that characterizes the dispersion of the values that could reasonably be attributed to the measurement. Got that? (Redundant question!)
Responsible Functions of Testing Bodies
Let’s start with the responsibility of functions:
Quality Assurance: QA is responsible for maintaining and performing the activities defined in the estimation of uncertainty in the measurement procedure.
Lab Operations: All Lab operators are responsible for ensuring that all the specified requirements should be followed by all means.
Other Supporting Functions: All other relevant functions are responsible for ensuring that all the requirements specified in the procedure has been fulfilled or not.
Why Calculate Uncertainty of Measurement?
The ultimate use of estimating uncertainties in measurement is to:
- Be able to exhibit about the accuracy of test results that have been performed in the lab by lab operators.
- Allow the consumer of data to be able to interpret data in the report properly.
While estimating the uncertainties, it is important to take into account all possible contributors that can affect your lab testing activity and on the uncertainty of measurement.
- After measuring uncertainty in measurement, one can get a realistic comparison of outcomes from different testing/calibration bodies.
- Measuring uncertainty in measurement often helps to avoid repetitive testing/calibration procedures, thus saving time and cost.
- While evaluating uncertainties in measurement, one always count all the factors that can impact or contribute towards uncertainties in measurement, leading to improvement of the procedures, making testing/calibration bodies more precise.
General Principles of Measuring Uncertainties of Measurement
- Know More About Measurand: The main objective of doing measurement is to know the value of measurand (anything which is being measured). It is important for measurement to begin with an appropriate set of specification of the measurand, a proper method of measurement, and the specific detail of the measurement procedure.
- Perfectly Perfect: No measurement process or testing /calibration can be called perfectly perfect! Also, those imperfections help uncertainties to rise ultimately leading to an error of measurement in the final result. The result of any measurement being carried out has some certain quantity of uncertainties, which are important to get identified.
- Components of Uncertainties: Random and Systematic components always exist in case of errors. However, uncertainties arise from more random factors and imperfect calibration for systematic errors.
- Random errors: Random errors usually arises from variations being made randomly. Every time a measurement is being done, random factors impact uncertainties in different ways, varying in every measurement cycle coming from various sources each time the measurement is being taken.
- Systematic errors: Systematic errors arise from other systematic effects. However, these can be reduced to a much extent firstly by identifying them and then by eliminating (preferably) or reducing them.
- Components of Uncertainty of Measurement: All the components of the uncertainty of measurement should be evaluated using proper methods, and each is expressed as Standard Deviation and also referred to as Standard Uncertainty.
- Standard Components of Uncertainties: All the standard components of uncertainties combined to produce an overall uncertainty value, which is often referred to as Combined Standard Uncertainty.
Where Does Uncertainty in Measurement Come From?
There can be many possible sources of uncertainties in testing/calibration and measurements existing in testing/calibration labs, which can be stated as:
- If the requirement of the test/calibration is not being defined clearly, then ambiguities may lead to uncertainties in measurement
- Even if the requirements of the test/calibration is known even then, it is not possible to fulfill the required conditions for the testing/calibration bodies
- Improper sampling methods may lead to uncertainties
- Especially in analog instruments, personal bias can end up having uncertainty in measurement
- The mistake in the values of constants and other parameters used in data evaluation
- Errors in instrument scale
- Variations in repeated observations can still be observed even if the test /calibration is being performed in the same conditions
Calibration is characterized as follows:
- Repeated measurements can be made
- Uncertainty of reference instruments is provided at each stage down the calibration chain, starting with the national standard, and
- Customers are aware of the need for a statement of uncertainty to ensure that the instrument meets their requirements.
Basic Calculations
The measurement uncertainty calculation is:
Expanded Uncertainty = (combined Standard Uncertainty) * K
Where K is the coverage factor.
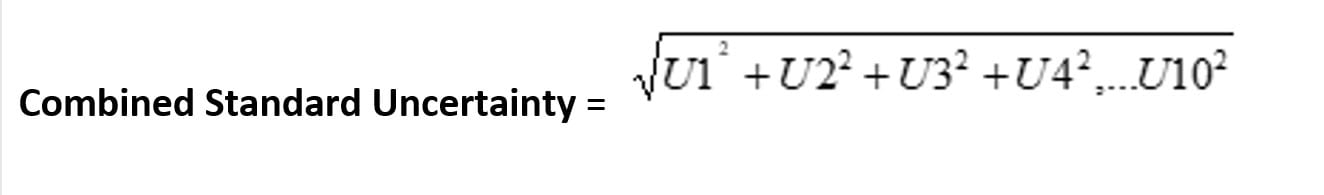
The combined Standard Uncertainty is an RSS (Root Sum Square) calculation:
U1 is the calibrator’s accuracy-related uncertainty.
U2 is the combination of two DUT related uncertainty components:
- S1: The standard deviation of the mean within a sequence of actual measurements (a Type A uncertainty)
- S2: The resolution (or sensitivity) of the DUT (a Type B uncertainty)
U3, U4, U5, U6, U7, U8, U9, and U10 are optional uncertainty components.
Uncertainty is an unpreventable part of any measurement, and it begins to matter when results are close to a specified limit. A proper evaluation of uncertainty is good professional testing/calibration body practice and can provide laboratories and customers with valuable information about the quality and reliability of the result.
Although common practice in calibration, there is some way to go with an expression of uncertainty in testing/calibration; however, there is growing activity in the area and, in time, estimation of uncertainty measurement will be common. No more WAGs!
Looking to get ISO/IEC 17025 accreditation for your business?
What questions do you have and how can we help?
